📄문제
왼쪽의 번호와 오른쪽의 번호가 있는 그림에서 같은 번호끼리 선으로 연결하려고 합니다.
왼쪽번호는 무조건 위에서부터 차례로 1부터 N까지 오름차순으로 나열되어 있습니다.
오른쪽의 번호 정보가 위부터 아래 순서로 주어지만 서로 선이 겹치지 않고 최대 몇 개의 선
을 연결할 수 있는 지 구하는 프로그램을 작성하세요.
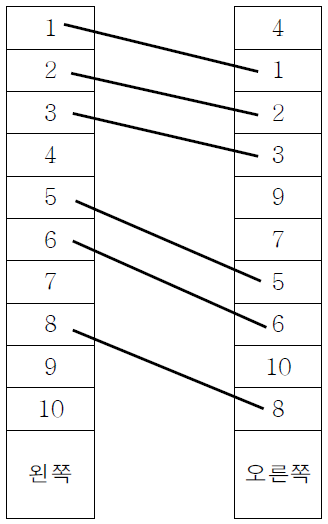
위의 그림은 오른쪽 번호 정보가 4 1 2 3 9 7 5 6 10 8 로 입력되었을 때 선이 서로 겹치지
않고 연결할 수 있는 최대 선을 개수 6을 구한 경우입니다.
⬇️ 입력
첫 줄에 자연수 N(1<=N<=100)이 주어집니다.
두 번째 줄에 1부터 N까지의 자연수 N개의 오른쪽 번호 정보가 주어집니다.
순서는 위쪽번호 부터 아래쪽번호 순으로입니다.
| 10 4 1 2 3 9 7 5 6 10 8 |
⬆️ 출력
첫 줄에 겹치지 않고 그을 수 있는 최대선의 개수를 출력합니다.
| 6 |
📝 풀이
#include <iostream>
using namespace std;
int dp[101];
int numbers[101];
int main()
{
int N, res = INT_MIN;
cin >> N;
for (int i = 0; i < N; ++i)
cin >> numbers[i];
dp[0] = 1;
for (int i = 1; i < N; ++i)
{
int max = 0;
for (int j = i - 1; j >= 0; --j)
{
if (numbers[i] > numbers[j])
{
if (max < dp[j])
max = dp[j];
}
}
dp[i] = max + 1;
if (res < dp[i])
res = dp[i];
}
cout << res;
}- 왼쪽 번호는 1부터 차례대로 되어있고, 오른쪽 번호는 입력에 따라 무작위로 설정됩니다.
- 이 문제에서 중요한것은, 차례대로 되어있는 왼쪽을 생각하여 오른쪽 번호가 "가장 긴 증가하는 부분 수열"을 만족하여 큰 값을 찾으면 된다는 것 입니다.
- 증가하는 부분 수열이 아닌경우, 선은 서로 교차될 수 밖에 없습니다.
- "가장 긴 증가하는 부분 수열"은 각 번호를 마지막부터 검사하여 앞 번호가 자신보다 작다면, 앞 번호가 가지고 있는 최대 순열의 수 + 1을 자신에게 저장하여 끝까지 검사하여 결과를 낼 수 있습니다.
'algorithms (C++)' 카테고리의 다른 글
| [C++] 알리바바와 40인의 도둑 (0) | 2023.10.20 |
|---|---|
| [C++] 가장 높은 탑 쌓기 🔥 (0) | 2023.10.20 |
| [C++] 최대 부분 증가수열 🔥 (0) | 2023.10.20 |
| [C++] 돌다리 건너기(Bottom-Up) (0) | 2023.10.20 |
| [C++] 계단오르기(Top-Down : 메모이제이션) (0) | 2023.10.20 |
📄문제
왼쪽의 번호와 오른쪽의 번호가 있는 그림에서 같은 번호끼리 선으로 연결하려고 합니다.
왼쪽번호는 무조건 위에서부터 차례로 1부터 N까지 오름차순으로 나열되어 있습니다.
오른쪽의 번호 정보가 위부터 아래 순서로 주어지만 서로 선이 겹치지 않고 최대 몇 개의 선
을 연결할 수 있는 지 구하는 프로그램을 작성하세요.

위의 그림은 오른쪽 번호 정보가 4 1 2 3 9 7 5 6 10 8 로 입력되었을 때 선이 서로 겹치지
않고 연결할 수 있는 최대 선을 개수 6을 구한 경우입니다.
⬇️ 입력
첫 줄에 자연수 N(1<=N<=100)이 주어집니다.
두 번째 줄에 1부터 N까지의 자연수 N개의 오른쪽 번호 정보가 주어집니다.
순서는 위쪽번호 부터 아래쪽번호 순으로입니다.
| 10 4 1 2 3 9 7 5 6 10 8 |
⬆️ 출력
첫 줄에 겹치지 않고 그을 수 있는 최대선의 개수를 출력합니다.
| 6 |
📝 풀이
#include <iostream>
using namespace std;
int dp[101];
int numbers[101];
int main()
{
int N, res = INT_MIN;
cin >> N;
for (int i = 0; i < N; ++i)
cin >> numbers[i];
dp[0] = 1;
for (int i = 1; i < N; ++i)
{
int max = 0;
for (int j = i - 1; j >= 0; --j)
{
if (numbers[i] > numbers[j])
{
if (max < dp[j])
max = dp[j];
}
}
dp[i] = max + 1;
if (res < dp[i])
res = dp[i];
}
cout << res;
}- 왼쪽 번호는 1부터 차례대로 되어있고, 오른쪽 번호는 입력에 따라 무작위로 설정됩니다.
- 이 문제에서 중요한것은, 차례대로 되어있는 왼쪽을 생각하여 오른쪽 번호가 "가장 긴 증가하는 부분 수열"을 만족하여 큰 값을 찾으면 된다는 것 입니다.
- 증가하는 부분 수열이 아닌경우, 선은 서로 교차될 수 밖에 없습니다.
- "가장 긴 증가하는 부분 수열"은 각 번호를 마지막부터 검사하여 앞 번호가 자신보다 작다면, 앞 번호가 가지고 있는 최대 순열의 수 + 1을 자신에게 저장하여 끝까지 검사하여 결과를 낼 수 있습니다.
'algorithms (C++)' 카테고리의 다른 글
| [C++] 알리바바와 40인의 도둑 (0) | 2023.10.20 |
|---|---|
| [C++] 가장 높은 탑 쌓기 🔥 (0) | 2023.10.20 |
| [C++] 최대 부분 증가수열 🔥 (0) | 2023.10.20 |
| [C++] 돌다리 건너기(Bottom-Up) (0) | 2023.10.20 |
| [C++] 계단오르기(Top-Down : 메모이제이션) (0) | 2023.10.20 |
