위상 정렬은 방향 그래프에서만 적용 가능합니다. 각 간선은 한 정점에서 다른 정점으로 방향을 가집니다.
위상 정렬은 주기(Cycle)가 없는 그래프에만 적용 가능합니다. 주기가 있는 그래프에서는 위상 정렬을 수행할 수 없습니다.
위상 정렬은 시작점이 없는 그래프에서 정점을 선형적으로 나열하는 작업입니다.
알고리즘은 각 정점의 진입 차수(In-Degree)를 계산하고, 진입 차수가 0인 정점을 시작으로 선택합니다.
선택한 정점을 결과로 나열하고, 그 정점과 연결된 간선을 제거한 후, 다음 진입 차수가 0인 정점을 선택합니다.
이 과정을 반복하여 모든 정점이 나열될 때까지 진행합니다.
📄문제
위상정렬은 어떤 일을 하는 순서를 찾는 알고리즘입니다.
각각의 일의 선후관계가 복잡하게 얽혀있을 때 각각 일의 선후관계를 유지하면서 전체 일의 순서를 짜는 알고리즘입니다.
만약 아래와 같은 일의 순서를 각각 지키면서 전체 일의 순서를 정한다면
1 4 //1번일을 하고 난 후 4번일을 해야한다.
5 4
4 3
2 5
2 3
6 2
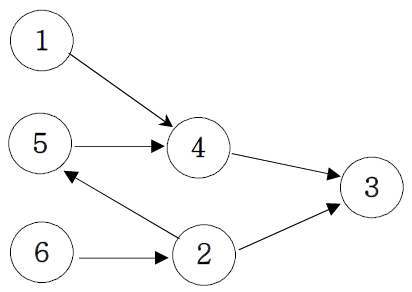
전체 일의 순서는 1, 6, 2, 5, 4, 3과 같이 정할 수 있다. 전체 일의 순서는 여러 가지가 있습니다 그 중에 하나입니다.
⬇️ 입력
첫 번째 줄에 전체 일의 개수 N과 일의 순서 정보의 개수 M이 주어집니다.
두 번째 줄부터 M개의 정보가 주어집니다.
| 6 6 1 4 5 4 4 3 2 5 2 3 6 2 |
⬆️ 출력
전체 일의 순서를 출력합니다.
| 1 6 2 5 4 3 |
📝 풀이
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
int n, m, a, b, score;
cin >> n >> m;
// 그래프 간선 정보를 저장
vector<vector<int> > graph(n + 1, vector<int>(n + 1, 0));
// 그래프의 차수를 저장
vector<int> degree(n + 1);
// 큐
queue<int> Q;
// 입력을 받아 그래프 간선 정보를 설정
for (int i = 0; i < m; i++)
{
cin >> a >> b;
graph[a][b] = 1;
// 입력에 대한 차수를 미리 증가시키기 (선행 작업이 있음)
degree[b]++;
}
// 차수가 0인 모든 간선을 삽입
for (int i = 1; i <= n; i++)
{
if (degree[i] == 0)
Q.push(i);
}
while (!Q.empty()) {
int now = Q.front();
Q.pop();
cout << now << " ";
// 현재 간선에서 다른 간선으로의 입력이 있다면, 해당 간선의 차수를 감소시킴
// 감소된 간선을 큐에 삽입하여 반복
for (int i = 1; i <= n; i++)
{
if (graph[now][i] == 1)
{
degree[i]--;
if (degree[i] == 0)
Q.push(i);
}
}
}
return 0;
}
'algorithms (C++)' 카테고리의 다른 글
| [C++][프로그래머스] 전국 대회 선발 고사 (0) | 2023.10.22 |
|---|---|
| [C++][프로그래머스] x 사이의 개수 (0) | 2023.10.22 |
| [C++] 회장뽑기(플로이드 워샬) 🔥 (0) | 2023.10.20 |
| [C++] 플로이드 워샬 알고리즘 ⭐ (0) | 2023.10.20 |
| [C++] 최대점수 구하기(냅색 알고리즘) 🔥 (0) | 2023.10.20 |
위상 정렬은 방향 그래프에서만 적용 가능합니다. 각 간선은 한 정점에서 다른 정점으로 방향을 가집니다.
위상 정렬은 주기(Cycle)가 없는 그래프에만 적용 가능합니다. 주기가 있는 그래프에서는 위상 정렬을 수행할 수 없습니다.
위상 정렬은 시작점이 없는 그래프에서 정점을 선형적으로 나열하는 작업입니다.
알고리즘은 각 정점의 진입 차수(In-Degree)를 계산하고, 진입 차수가 0인 정점을 시작으로 선택합니다.
선택한 정점을 결과로 나열하고, 그 정점과 연결된 간선을 제거한 후, 다음 진입 차수가 0인 정점을 선택합니다.
이 과정을 반복하여 모든 정점이 나열될 때까지 진행합니다.
📄문제
위상정렬은 어떤 일을 하는 순서를 찾는 알고리즘입니다.
각각의 일의 선후관계가 복잡하게 얽혀있을 때 각각 일의 선후관계를 유지하면서 전체 일의 순서를 짜는 알고리즘입니다.
만약 아래와 같은 일의 순서를 각각 지키면서 전체 일의 순서를 정한다면
1 4 //1번일을 하고 난 후 4번일을 해야한다.
5 4
4 3
2 5
2 3
6 2

전체 일의 순서는 1, 6, 2, 5, 4, 3과 같이 정할 수 있다. 전체 일의 순서는 여러 가지가 있습니다 그 중에 하나입니다.
⬇️ 입력
첫 번째 줄에 전체 일의 개수 N과 일의 순서 정보의 개수 M이 주어집니다.
두 번째 줄부터 M개의 정보가 주어집니다.
| 6 6 1 4 5 4 4 3 2 5 2 3 6 2 |
⬆️ 출력
전체 일의 순서를 출력합니다.
| 1 6 2 5 4 3 |
📝 풀이
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
int n, m, a, b, score;
cin >> n >> m;
// 그래프 간선 정보를 저장
vector<vector<int> > graph(n + 1, vector<int>(n + 1, 0));
// 그래프의 차수를 저장
vector<int> degree(n + 1);
// 큐
queue<int> Q;
// 입력을 받아 그래프 간선 정보를 설정
for (int i = 0; i < m; i++)
{
cin >> a >> b;
graph[a][b] = 1;
// 입력에 대한 차수를 미리 증가시키기 (선행 작업이 있음)
degree[b]++;
}
// 차수가 0인 모든 간선을 삽입
for (int i = 1; i <= n; i++)
{
if (degree[i] == 0)
Q.push(i);
}
while (!Q.empty()) {
int now = Q.front();
Q.pop();
cout << now << " ";
// 현재 간선에서 다른 간선으로의 입력이 있다면, 해당 간선의 차수를 감소시킴
// 감소된 간선을 큐에 삽입하여 반복
for (int i = 1; i <= n; i++)
{
if (graph[now][i] == 1)
{
degree[i]--;
if (degree[i] == 0)
Q.push(i);
}
}
}
return 0;
}
'algorithms (C++)' 카테고리의 다른 글
| [C++][프로그래머스] 전국 대회 선발 고사 (0) | 2023.10.22 |
|---|---|
| [C++][프로그래머스] x 사이의 개수 (0) | 2023.10.22 |
| [C++] 회장뽑기(플로이드 워샬) 🔥 (0) | 2023.10.20 |
| [C++] 플로이드 워샬 알고리즘 ⭐ (0) | 2023.10.20 |
| [C++] 최대점수 구하기(냅색 알고리즘) 🔥 (0) | 2023.10.20 |
