플로이드-와샬(Floyd-Warshall) 알고리즘은 그래프 내의 모든 노드 쌍 간의 최단 경로를 찾는 알고리즘입니다. 특히 음수 가중치와 음수 가중치 사이클을 포함하는 그래프에서도 동작합니다. 플로이드-와샬 알고리즘은 동적 계획법(Dynamic Programming)을 기반으로 합니다.
플로이드-와샬 알고리즘은 음수 가중치와 음수 가중치 사이클을 다룰 수 있습니다. 물론 음수 가중치 사이클이 없는 경우에만 올바른 결과를 얻을 수 있습니다.
알고리즘의 시간 복잡도는 O(N^3)로, 노드의 수에 대해 세제곱 시간이 소요됩니다. 따라서 큰 그래프에서는 실행 시간이 길어질 수 있습니다.
결과 배열에는 모든 노드 쌍 간의 최단 경로가 저장되며, 노드 쌍 간의 최단 경로를 직접 액세스할 수 있습니다.
📄문제
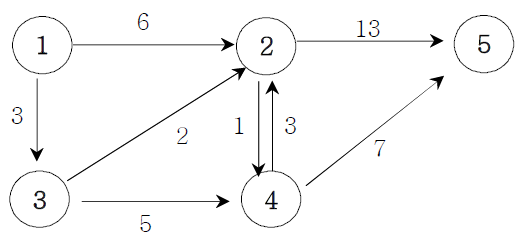
N개의 도시가 주어지고, 각 도시들을 연결하는 도로와 해당 도로를 통행하는 비용이 주어질 때 모든 도시에서 모든 도시로 이동하는데 쓰이는 비용의 최소값을 구하는 프로그램을 작성하세요.
⬇️ 입력
첫 번째 줄에는 도시의 수N(N<=100)과 도로수 M(M<=200)가 주어지고, M줄에 걸쳐 도로정보와 비용(20 이하의 자연수)이 주어진다. 만약 1번 도시와 2번도시가 연결되고 그 비용이 13이면 “1 2 13”으로 주어진다.
⬆️ 출력
모든 도시에서 모든 도시로 이동하는데 드는 최소 비용을 아래와 같이 출력한다.
자기자신으로 가는 비용은 0입니다. i번 정점에서 j번 정점으로 갈 수 없을 때는 비용을 “M"으로 출력합니다.
📝 풀이
#include<iostream>
#include<vector>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
int n, m, a, b, c;
cin >> n >> m;
vector<vector<int> > dis(n + 1, vector<int>(n + 1, 5000));
// 자기 자신에 대한 비용은 0
for (int i = 1; i <= n; i++)
dis[i][i] = 0;
// 바로 갈 수 있는 노드는 미리 값을 적어두기
for (int i = 1; i <= m; i++)
{
cin >> a >> b >> c;
dis[a][b] = c;
}
// 플로이드 와샬
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
{
// 기존 값 dis[i][j]보다 dis[i][k] + dis[k][j]가 더 적다면?
// 기존 저장된 값보다, i -> k -> j가 더 비용이 낮으면?
dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
if (dis[i][j] == 5000)
{
cout << "M ";
}
else cout << dis[i][j] << " ";
}
cout << endl;
}
return 0;
}- 코드의 가장 바깥쪽 for 루프는 중간 노드 k를 선택합니다. k는 1부터 n까지의 모든 노드를 순회하며, n은 전체 노드의 수를 나타냅니다.
- 중첩된 두 개의 for 루프는 모든 노드 i와 j에 대해 최단 경로를 검사합니다. 이 두 중첩된 루프는 중간 노드 k에 대한 최단 경로를 계산하고, 이를 모든 노드 i와 j에 대해 반복합니다.
'algorithms (C++)' 카테고리의 다른 글
| [C++] 위상정렬(그래프 정렬) ⭐ (0) | 2023.10.20 |
|---|---|
| [C++] 회장뽑기(플로이드 워샬) 🔥 (0) | 2023.10.20 |
| [C++] 최대점수 구하기(냅색 알고리즘) 🔥 (0) | 2023.10.20 |
| [C++] 동전교환 ⭐ (0) | 2023.10.20 |
| [C++] 가방문제(냅색 알고리즘) ⭐ (0) | 2023.10.20 |
