프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
📄 문제
N개의 마을로 이루어진 나라가 있습니다. 이 나라의 각 마을에는 1부터 N까지의 번호가 각각 하나씩 부여되어 있습니다. 각 마을은 양방향으로 통행할 수 있는 도로로 연결되어 있는데, 서로 다른 마을 간에 이동할 때는 이 도로를 지나야 합니다. 도로를 지날 때 걸리는 시간은 도로별로 다릅니다. 현재 1번 마을에 있는 음식점에서 각 마을로 음식 배달을 하려고 합니다. 각 마을로부터 음식 주문을 받으려고 하는데, N개의 마을 중에서 K 시간 이하로 배달이 가능한 마을에서만 주문을 받으려고 합니다. 다음은 N = 5, K = 3인 경우의 예시입니다.
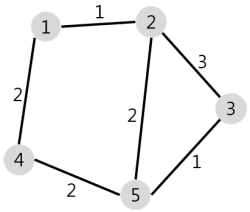
위 그림에서 1번 마을에 있는 음식점은 [1, 2, 4, 5] 번 마을까지는 3 이하의 시간에 배달할 수 있습니다. 그러나 3번 마을까지는 3시간 이내로 배달할 수 있는 경로가 없으므로 3번 마을에서는 주문을 받지 않습니다. 따라서 1번 마을에 있는 음식점이 배달 주문을 받을 수 있는 마을은 4개가 됩니다.
마을의 개수 N, 각 마을을 연결하는 도로의 정보 road, 음식 배달이 가능한 시간 K가 매개변수로 주어질 때, 음식 주문을 받을 수 있는 마을의 개수를 return 하도록 solution 함수를 완성해주세요.
📝 풀이
다익스트라 알고리즘
적용 시점: 음의 가중치를 갖지 않는 그래프에 적합합니다. 각 간선의 가중치는 양수여야 합니다.
동작 방식: 시작 노드로부터 다른 모든 노드까지의 최단 경로를 찾을 때 사용됩니다.
작동 방식: 각 노드마다 최단 거리를 저장하면서, 해당 노드와 연결된 간선을 탐색하며 최단 거리를 업데이트합니다. 이를 위해 우선순위 큐를 사용하여 현재까지의 최단 거리를 계산하여 처리합니다.
시간 복잡도: 힙(우선순위 큐)을 사용하므로 O((V + E)logV)의 시간 복잡도를 가집니다. (V: 노드 수, E: 간선 수)
벨만-포드 알고리즘
적용 시점: 음의 가중치를 포함하거나 음수 사이클이 있는 경우에 사용됩니다. 음수 사이클이 없는 경우에도 사용 가능하지만, 다익스트라보다 느린 성능을 보입니다.
동작 방식: 모든 간선을 순회하면서 최단 경로를 찾습니다. 각 노드를 반복해서 거치며 최단 거리를 업데이트합니다. 음수 사이클을 탐지할 수 있습니다.
작동 방식: 간선을 모든 노드 수 - 1만큼 반복하여 최단 거리를 찾습니다. 모든 노드 쌍에 대한 최단 거리를 확인하기 위해 사용될 수 있습니다.
시간 복잡도: O(VE)의 시간 복잡도를 가집니다. (V: 노드 수, E: 간선 수)
어느 시점에서 사용하는가?
다익스트라 알고리즘은 음의 가중치가 없는 그래프에서 최단 거리를 찾을 때 적합합니다.
벨만-포드 알고리즘은 음의 가중치가 있거나 음수 사이클을 탐지해야 할 때 사용됩니다. 또한, 모든 노드 쌍에 대한 최단 경로를 확인할 때에도 사용될 수 있습니다.
요약하자면, 음의 가중치가 없는 경우에는 다익스트라 알고리즘이 효율적입니다. 그러나 음수 가중치가 있거나 음수 사이클을 확인해야 하는 경우에는 벨만-포드 알고리즘이 더 적합합니다.
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
// 간선 정보
struct Edge {
int from, to, weight;
};
int solution(int N, vector<vector<int>> road, int K) {
vector<Edge> edges;
vector<int> dist(N + 1, INT_MAX);
// 그래프 정보 초기화 (무방향 그래프로 양측 노드에 삽입)
for (vector<int> r : road) {
edges.push_back({ r[0], r[1], r[2] });
edges.push_back({ r[1], r[0], r[2] });
}
// 시작 노드의 거리는 0
dist[1] = 0;
// 벨만-포드 알고리즘
// 모든 노드에 대한 가장 짧은 경로는 노드의 수보다 하나 작은 간선의 수(N-1)로 이루어지기에 N-1번 반복
for (int i = 0; i < N - 1; ++i)
for (Edge edge : edges)
{
int from = edge.from;
int to = edge.to;
int weight = edge.weight;
// 아직 다른 간선에 의해 비용이 계산되지 않은경우에는 무시
if(dist[from] == INT_MAX)
continue;
// 현재 위치의 비용(dist[from]) + 다음 위치까지의 비용(weight)이 저장된 비용(dist[to])보다 작으면 갱신
dist[to] = min(dist[to], dist[from] + weight);
}
// 정답 구하기
int answer = 0;
for(int i = 1; i <= N; ++i)
if(dist[i] <= K)
++answer;
return answer;
}#include <iostream>
#include <vector>
#include <climits>
using namespace std;
struct Edge {
int from, to, weight;
};
int solution(int N, vector<vector<int>> road, int K) {
vector<Edge> graph;
for(vector<int>& v : road)
{
graph.push_back({v[0], v[1], v[2]});
graph.push_back({v[1], v[0], v[2]});
}
vector<int> dist(N + 1, INT_MAX);
dist[1] = 0; // 시작 지점은 거리가 0으로 시작
// N-1만큼 반복한 후, 음의 사이클을 검사하기위해 한번 더 검사(<=로 표현)
for (int i = 0; i <= N - 1; ++i) {
for (Edge& edge : graph) {
int from = edge.from;
int to = edge.to;
int weight = edge.weight;
if(dist[from] == INT_MAX)
continue;
// 음의 사이클을 검사
// N-1번째에도 dist[from] + weight < dist[to]가 참이라면, 음의 사이클이 존재
if(i == N - 1 && dist[from] + weight < dist[to])
return -1;
dist[to] = min(dist[to], dist[from] + weight);
}
}
// 정답 구하기
int answer = 0;
for(int i = 1; i <= N; ++i)
if(dist[i] <= K)
++answer;
return answer;
}
- 벨만 포드 알고리즘을 활용하여 문제를 해결하였습니다.
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
using namespace std;
// 간선 정보
struct Edge {
int to, weight;
};
int solution(int N, vector<vector<int>> road, int K) {
vector<vector<Edge>> graph(N + 1);
vector<int> dist(N + 1, INT_MAX);
// 그래프 정보 초기화 (양방향)
for (vector<int> r : road) {
int from = r[0];
int to = r[1];
int weight = r[2];
graph[from].push_back({to, weight});
graph[to].push_back({from, weight});
}
// 우선순위 큐를 이용한 다익스트라 알고리즘
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
dist[1] = 0; // 시작 노드의 거리는 0
pq.push({0, 1}); // {거리, 노드} 쌍을 우선순위 큐에 삽입
while (!pq.empty()) {
int current_distance = pq.top().first;
int current_node = pq.top().second;
pq.pop();
// 현재 노드에서 갈 수 있는 모든 노드들에 대해 최단 거리 갱신
for (Edge& e : graph[current_node]) {
int next_node = e.to;
int weight = e.weight;
if (dist[next_node] > current_distance + weight) {
dist[next_node] = current_distance + weight;
pq.push({dist[next_node], next_node});
}
}
}
// 정답 구하기
int answer = 0;
for (int i = 1; i <= N; ++i)
if (dist[i] <= K)
++answer;
return answer;
}#include <iostream>
#include <vector>
#include <queue>
#include <climits>
using namespace std;
int solution(int N, vector<vector<int> > road, int K) {
vector<vector<pair<int, int>>> graph(N + 1, vector<pair<int, int>>());
for(vector<int>& v : road)
{
graph[v[0]].push_back({v[1], v[2]});
graph[v[1]].push_back({v[0], v[2]});
}
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
vector<int> dist(N + 1, INT_MAX);
pq.push({0, 1});
dist[1] = 0;
while(!pq.empty())
{
int currentDistance = pq.top().first; // 현재 노드까지의 누적 가중치
int currentNode = pq.top().second; // 현재 노드 위치
pq.pop();
// 현재 노드를 기준으로 갈 수 있는 모든 경로를 반복
for(pair<int, int>& p : graph[currentNode])
{
int nextNode = p.first; // 다음 노드의 번호
int weight = p.second; // 다음 노드로 가기까지 가중치
// 현재 노드까지의 가중치 + 다음 노드 가중치가 저장된 값보다 더 작다면?
if(dist[nextNode] > currentDistance + weight)
{
dist[nextNode] = currentDistance + weight; // 값을 갱신
pq.push({dist[nextNode], nextNode}); // 큐에 가중치와 다음노드 번호를 삽입
}
}
}
// 정답 구하기
int answer = 0;
for (int i = 1; i <= N; ++i)
if (dist[i] <= K)
++answer;
return answer;
}
- 다익스트라 알고리즘을 이용하여 문제를 해결하였습니다.
'algorithms (C++)' 카테고리의 다른 글
| [C++][프로그래머스] 게임 맵 최단거리 (1) | 2023.11.20 |
|---|---|
| [C++][프로그래머스] 가장 큰 정사각형 찾기 (1) | 2023.11.20 |
| [C++][프로그래머스] [1차] 프렌즈4블록 (1) | 2023.11.19 |
| [C++] 코딩테스트 유용한 함수 및 표현 정리 📖 (0) | 2023.11.19 |
| [C++][프로그래머스] [1차] 캐시 (0) | 2023.11.19 |
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
📄 문제
N개의 마을로 이루어진 나라가 있습니다. 이 나라의 각 마을에는 1부터 N까지의 번호가 각각 하나씩 부여되어 있습니다. 각 마을은 양방향으로 통행할 수 있는 도로로 연결되어 있는데, 서로 다른 마을 간에 이동할 때는 이 도로를 지나야 합니다. 도로를 지날 때 걸리는 시간은 도로별로 다릅니다. 현재 1번 마을에 있는 음식점에서 각 마을로 음식 배달을 하려고 합니다. 각 마을로부터 음식 주문을 받으려고 하는데, N개의 마을 중에서 K 시간 이하로 배달이 가능한 마을에서만 주문을 받으려고 합니다. 다음은 N = 5, K = 3인 경우의 예시입니다.

위 그림에서 1번 마을에 있는 음식점은 [1, 2, 4, 5] 번 마을까지는 3 이하의 시간에 배달할 수 있습니다. 그러나 3번 마을까지는 3시간 이내로 배달할 수 있는 경로가 없으므로 3번 마을에서는 주문을 받지 않습니다. 따라서 1번 마을에 있는 음식점이 배달 주문을 받을 수 있는 마을은 4개가 됩니다.
마을의 개수 N, 각 마을을 연결하는 도로의 정보 road, 음식 배달이 가능한 시간 K가 매개변수로 주어질 때, 음식 주문을 받을 수 있는 마을의 개수를 return 하도록 solution 함수를 완성해주세요.
📝 풀이
다익스트라 알고리즘
적용 시점: 음의 가중치를 갖지 않는 그래프에 적합합니다. 각 간선의 가중치는 양수여야 합니다.
동작 방식: 시작 노드로부터 다른 모든 노드까지의 최단 경로를 찾을 때 사용됩니다.
작동 방식: 각 노드마다 최단 거리를 저장하면서, 해당 노드와 연결된 간선을 탐색하며 최단 거리를 업데이트합니다. 이를 위해 우선순위 큐를 사용하여 현재까지의 최단 거리를 계산하여 처리합니다.
시간 복잡도: 힙(우선순위 큐)을 사용하므로 O((V + E)logV)의 시간 복잡도를 가집니다. (V: 노드 수, E: 간선 수)
벨만-포드 알고리즘
적용 시점: 음의 가중치를 포함하거나 음수 사이클이 있는 경우에 사용됩니다. 음수 사이클이 없는 경우에도 사용 가능하지만, 다익스트라보다 느린 성능을 보입니다.
동작 방식: 모든 간선을 순회하면서 최단 경로를 찾습니다. 각 노드를 반복해서 거치며 최단 거리를 업데이트합니다. 음수 사이클을 탐지할 수 있습니다.
작동 방식: 간선을 모든 노드 수 - 1만큼 반복하여 최단 거리를 찾습니다. 모든 노드 쌍에 대한 최단 거리를 확인하기 위해 사용될 수 있습니다.
시간 복잡도: O(VE)의 시간 복잡도를 가집니다. (V: 노드 수, E: 간선 수)
어느 시점에서 사용하는가?
다익스트라 알고리즘은 음의 가중치가 없는 그래프에서 최단 거리를 찾을 때 적합합니다.
벨만-포드 알고리즘은 음의 가중치가 있거나 음수 사이클을 탐지해야 할 때 사용됩니다. 또한, 모든 노드 쌍에 대한 최단 경로를 확인할 때에도 사용될 수 있습니다.
요약하자면, 음의 가중치가 없는 경우에는 다익스트라 알고리즘이 효율적입니다. 그러나 음수 가중치가 있거나 음수 사이클을 확인해야 하는 경우에는 벨만-포드 알고리즘이 더 적합합니다.
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
// 간선 정보
struct Edge {
int from, to, weight;
};
int solution(int N, vector<vector<int>> road, int K) {
vector<Edge> edges;
vector<int> dist(N + 1, INT_MAX);
// 그래프 정보 초기화 (무방향 그래프로 양측 노드에 삽입)
for (vector<int> r : road) {
edges.push_back({ r[0], r[1], r[2] });
edges.push_back({ r[1], r[0], r[2] });
}
// 시작 노드의 거리는 0
dist[1] = 0;
// 벨만-포드 알고리즘
// 모든 노드에 대한 가장 짧은 경로는 노드의 수보다 하나 작은 간선의 수(N-1)로 이루어지기에 N-1번 반복
for (int i = 0; i < N - 1; ++i)
for (Edge edge : edges)
{
int from = edge.from;
int to = edge.to;
int weight = edge.weight;
// 아직 다른 간선에 의해 비용이 계산되지 않은경우에는 무시
if(dist[from] == INT_MAX)
continue;
// 현재 위치의 비용(dist[from]) + 다음 위치까지의 비용(weight)이 저장된 비용(dist[to])보다 작으면 갱신
dist[to] = min(dist[to], dist[from] + weight);
}
// 정답 구하기
int answer = 0;
for(int i = 1; i <= N; ++i)
if(dist[i] <= K)
++answer;
return answer;
}#include <iostream>
#include <vector>
#include <climits>
using namespace std;
struct Edge {
int from, to, weight;
};
int solution(int N, vector<vector<int>> road, int K) {
vector<Edge> graph;
for(vector<int>& v : road)
{
graph.push_back({v[0], v[1], v[2]});
graph.push_back({v[1], v[0], v[2]});
}
vector<int> dist(N + 1, INT_MAX);
dist[1] = 0; // 시작 지점은 거리가 0으로 시작
// N-1만큼 반복한 후, 음의 사이클을 검사하기위해 한번 더 검사(<=로 표현)
for (int i = 0; i <= N - 1; ++i) {
for (Edge& edge : graph) {
int from = edge.from;
int to = edge.to;
int weight = edge.weight;
if(dist[from] == INT_MAX)
continue;
// 음의 사이클을 검사
// N-1번째에도 dist[from] + weight < dist[to]가 참이라면, 음의 사이클이 존재
if(i == N - 1 && dist[from] + weight < dist[to])
return -1;
dist[to] = min(dist[to], dist[from] + weight);
}
}
// 정답 구하기
int answer = 0;
for(int i = 1; i <= N; ++i)
if(dist[i] <= K)
++answer;
return answer;
}
- 벨만 포드 알고리즘을 활용하여 문제를 해결하였습니다.
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
using namespace std;
// 간선 정보
struct Edge {
int to, weight;
};
int solution(int N, vector<vector<int>> road, int K) {
vector<vector<Edge>> graph(N + 1);
vector<int> dist(N + 1, INT_MAX);
// 그래프 정보 초기화 (양방향)
for (vector<int> r : road) {
int from = r[0];
int to = r[1];
int weight = r[2];
graph[from].push_back({to, weight});
graph[to].push_back({from, weight});
}
// 우선순위 큐를 이용한 다익스트라 알고리즘
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
dist[1] = 0; // 시작 노드의 거리는 0
pq.push({0, 1}); // {거리, 노드} 쌍을 우선순위 큐에 삽입
while (!pq.empty()) {
int current_distance = pq.top().first;
int current_node = pq.top().second;
pq.pop();
// 현재 노드에서 갈 수 있는 모든 노드들에 대해 최단 거리 갱신
for (Edge& e : graph[current_node]) {
int next_node = e.to;
int weight = e.weight;
if (dist[next_node] > current_distance + weight) {
dist[next_node] = current_distance + weight;
pq.push({dist[next_node], next_node});
}
}
}
// 정답 구하기
int answer = 0;
for (int i = 1; i <= N; ++i)
if (dist[i] <= K)
++answer;
return answer;
}#include <iostream>
#include <vector>
#include <queue>
#include <climits>
using namespace std;
int solution(int N, vector<vector<int> > road, int K) {
vector<vector<pair<int, int>>> graph(N + 1, vector<pair<int, int>>());
for(vector<int>& v : road)
{
graph[v[0]].push_back({v[1], v[2]});
graph[v[1]].push_back({v[0], v[2]});
}
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
vector<int> dist(N + 1, INT_MAX);
pq.push({0, 1});
dist[1] = 0;
while(!pq.empty())
{
int currentDistance = pq.top().first; // 현재 노드까지의 누적 가중치
int currentNode = pq.top().second; // 현재 노드 위치
pq.pop();
// 현재 노드를 기준으로 갈 수 있는 모든 경로를 반복
for(pair<int, int>& p : graph[currentNode])
{
int nextNode = p.first; // 다음 노드의 번호
int weight = p.second; // 다음 노드로 가기까지 가중치
// 현재 노드까지의 가중치 + 다음 노드 가중치가 저장된 값보다 더 작다면?
if(dist[nextNode] > currentDistance + weight)
{
dist[nextNode] = currentDistance + weight; // 값을 갱신
pq.push({dist[nextNode], nextNode}); // 큐에 가중치와 다음노드 번호를 삽입
}
}
}
// 정답 구하기
int answer = 0;
for (int i = 1; i <= N; ++i)
if (dist[i] <= K)
++answer;
return answer;
}
- 다익스트라 알고리즘을 이용하여 문제를 해결하였습니다.
'algorithms (C++)' 카테고리의 다른 글
| [C++][프로그래머스] 게임 맵 최단거리 (1) | 2023.11.20 |
|---|---|
| [C++][프로그래머스] 가장 큰 정사각형 찾기 (1) | 2023.11.20 |
| [C++][프로그래머스] [1차] 프렌즈4블록 (1) | 2023.11.19 |
| [C++] 코딩테스트 유용한 함수 및 표현 정리 📖 (0) | 2023.11.19 |
| [C++][프로그래머스] [1차] 캐시 (0) | 2023.11.19 |
