📄 문제
ROR 게임은 두 팀으로 나누어서 진행하며, 상대 팀 진영을 먼저 파괴하면 이기는 게임입니다. 따라서, 각 팀은 상대 팀 진영에 최대한 빨리 도착하는 것이 유리합니다.
지금부터 당신은 한 팀의 팀원이 되어 게임을 진행하려고 합니다. 다음은 5 x 5 크기의 맵에, 당신의 캐릭터가 (행: 1, 열: 1) 위치에 있고, 상대 팀 진영은 (행: 5, 열: 5) 위치에 있는 경우의 예시입니다.
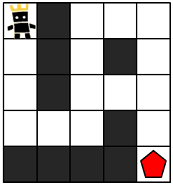
위 그림에서 검은색 부분은 벽으로 막혀있어 갈 수 없는 길이며, 흰색 부분은 갈 수 있는 길입니다. 캐릭터가 움직일 때는 동, 서, 남, 북 방향으로 한 칸씩 이동하며, 게임 맵을 벗어난 길은 갈 수 없습니다.
아래 예시는 캐릭터가 상대 팀 진영으로 가는 두 가지 방법을 나타내고 있습니다.
첫 번째 방법은 11개의 칸을 지나서 상대 팀 진영에 도착했습니다.

두 번째 방법은 15개의 칸을 지나서 상대팀 진영에 도착했습니다.

위 예시에서는 첫 번째 방법보다 더 빠르게 상대팀 진영에 도착하는 방법은 없으므로, 이 방법이 상대 팀 진영으로 가는 가장 빠른 방법입니다.
만약, 상대 팀이 자신의 팀 진영 주위에 벽을 세워두었다면 상대 팀 진영에 도착하지 못할 수도 있습니다. 예를 들어, 다음과 같은 경우에 당신의 캐릭터는 상대 팀 진영에 도착할 수 없습니다.

게임 맵의 상태 maps가 매개변수로 주어질 때, 캐릭터가 상대 팀 진영에 도착하기 위해서 지나가야 하는 칸의 개수의 최솟값을 return 하도록 solution 함수를 완성해주세요. 단, 상대 팀 진영에 도착할 수 없을 때는 -1을 return 해주세요.
📝 풀이
#include<vector>
#include<queue>
using namespace std;
int dx[4] { -1, 1, 0, 0};
int dy[4] { 0, 0, -1, 1};
int solution(vector<vector<int> > maps)
{
int row = maps.size();
int col = maps[0].size();
vector<vector<int>> dist(row, vector<int>(col, -1));
queue<pair<int, int>> q;
q.push({0, 0});
dist[0][0] = 1;
while(!q.empty())
{
int y = q.front().first;
int x = q.front().second;
q.pop();
for(int i = 0; i < 4; ++i)
{
int yy = y + dy[i];
int xx = x + dx[i];
if(xx == -1 || yy == -1 || xx == col || yy == row || maps[yy][xx] == 0 || dist[yy][xx] != -1)
continue;
q.push({yy, xx});
dist[yy][xx] = dist[y][x] + 1;
}
}
return dist[row - 1][col - 1];
}- BFS를 이용하여 문제를 해결할 수 있습니다.
- 2차원 벡터 dist를 이용하여 누적 거리를 검사합니다.
- 현재 위치 {y, x}에서 네 방향을 검사합니다.
- 만약 해당 위치가 map을 벗어나거나, 이미 다른 방법에 의해 도달한적이 있어 dist가 초기값인 -1이 아니라면 해당 경로로 검사하지 않습니다. 이 이유는 Queue의 특성으로, 이전에 이미 도달한 위치라면 이보다 최선의 값이 갱신될 수 없기 때문입니다.(선입선출)
- 목적지인 {row -1, col -1}위치의 dist를 리턴합니다.
'algorithms (C++)' 카테고리의 다른 글
| [C++][프로그래머스] 숫자 타자 대회 🔥 (1) | 2023.11.25 |
|---|---|
| [C++][프로그래머스] 단체사진 찍기 (1) | 2023.11.20 |
| [C++][프로그래머스] 가장 큰 정사각형 찾기 (1) | 2023.11.20 |
| [C++][프로그래머스] 배달 ⭐️ (0) | 2023.11.19 |
| [C++][프로그래머스] [1차] 프렌즈4블록 (1) | 2023.11.19 |
📄 문제
ROR 게임은 두 팀으로 나누어서 진행하며, 상대 팀 진영을 먼저 파괴하면 이기는 게임입니다. 따라서, 각 팀은 상대 팀 진영에 최대한 빨리 도착하는 것이 유리합니다.
지금부터 당신은 한 팀의 팀원이 되어 게임을 진행하려고 합니다. 다음은 5 x 5 크기의 맵에, 당신의 캐릭터가 (행: 1, 열: 1) 위치에 있고, 상대 팀 진영은 (행: 5, 열: 5) 위치에 있는 경우의 예시입니다.

위 그림에서 검은색 부분은 벽으로 막혀있어 갈 수 없는 길이며, 흰색 부분은 갈 수 있는 길입니다. 캐릭터가 움직일 때는 동, 서, 남, 북 방향으로 한 칸씩 이동하며, 게임 맵을 벗어난 길은 갈 수 없습니다.
아래 예시는 캐릭터가 상대 팀 진영으로 가는 두 가지 방법을 나타내고 있습니다.
첫 번째 방법은 11개의 칸을 지나서 상대 팀 진영에 도착했습니다.

두 번째 방법은 15개의 칸을 지나서 상대팀 진영에 도착했습니다.

위 예시에서는 첫 번째 방법보다 더 빠르게 상대팀 진영에 도착하는 방법은 없으므로, 이 방법이 상대 팀 진영으로 가는 가장 빠른 방법입니다.
만약, 상대 팀이 자신의 팀 진영 주위에 벽을 세워두었다면 상대 팀 진영에 도착하지 못할 수도 있습니다. 예를 들어, 다음과 같은 경우에 당신의 캐릭터는 상대 팀 진영에 도착할 수 없습니다.

게임 맵의 상태 maps가 매개변수로 주어질 때, 캐릭터가 상대 팀 진영에 도착하기 위해서 지나가야 하는 칸의 개수의 최솟값을 return 하도록 solution 함수를 완성해주세요. 단, 상대 팀 진영에 도착할 수 없을 때는 -1을 return 해주세요.
📝 풀이
#include<vector>
#include<queue>
using namespace std;
int dx[4] { -1, 1, 0, 0};
int dy[4] { 0, 0, -1, 1};
int solution(vector<vector<int> > maps)
{
int row = maps.size();
int col = maps[0].size();
vector<vector<int>> dist(row, vector<int>(col, -1));
queue<pair<int, int>> q;
q.push({0, 0});
dist[0][0] = 1;
while(!q.empty())
{
int y = q.front().first;
int x = q.front().second;
q.pop();
for(int i = 0; i < 4; ++i)
{
int yy = y + dy[i];
int xx = x + dx[i];
if(xx == -1 || yy == -1 || xx == col || yy == row || maps[yy][xx] == 0 || dist[yy][xx] != -1)
continue;
q.push({yy, xx});
dist[yy][xx] = dist[y][x] + 1;
}
}
return dist[row - 1][col - 1];
}- BFS를 이용하여 문제를 해결할 수 있습니다.
- 2차원 벡터 dist를 이용하여 누적 거리를 검사합니다.
- 현재 위치 {y, x}에서 네 방향을 검사합니다.
- 만약 해당 위치가 map을 벗어나거나, 이미 다른 방법에 의해 도달한적이 있어 dist가 초기값인 -1이 아니라면 해당 경로로 검사하지 않습니다. 이 이유는 Queue의 특성으로, 이전에 이미 도달한 위치라면 이보다 최선의 값이 갱신될 수 없기 때문입니다.(선입선출)
- 목적지인 {row -1, col -1}위치의 dist를 리턴합니다.
'algorithms (C++)' 카테고리의 다른 글
| [C++][프로그래머스] 숫자 타자 대회 🔥 (1) | 2023.11.25 |
|---|---|
| [C++][프로그래머스] 단체사진 찍기 (1) | 2023.11.20 |
| [C++][프로그래머스] 가장 큰 정사각형 찾기 (1) | 2023.11.20 |
| [C++][프로그래머스] 배달 ⭐️ (0) | 2023.11.19 |
| [C++][프로그래머스] [1차] 프렌즈4블록 (1) | 2023.11.19 |
