프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
📄 문제
인천 앞바다에는 1부터 n까지 서로 다른 번호가 매겨진 등대 n개가 존재합니다. 등대와 등대 사이를 오가는 뱃길이 n-1개 존재하여, 어느 등대에서 출발해도 다른 모든 등대까지 이동할 수 있습니다. 등대 관리자 윤성이는 전력을 아끼기 위하여, 이 중 몇 개의 등대만 켜 두려고 합니다. 하지만 등대를 아무렇게나 꺼버리면, 뱃길을 오가는 배들이 위험할 수 있습니다. 한 뱃길의 양쪽 끝 등대 중 적어도 하나는 켜져 있도록 등대를 켜 두어야 합니다.
예를 들어, 아래 그림과 같이 등대 8개와 7개의 뱃길들이 있다고 합시다. 이 경우 1번 등대와 5번 등대 두 개만 켜 두어도 모든 뱃길은 양쪽 끝 등대 중 하나가 켜져 있으므로, 배들은 안전하게 운항할 수 있습니다.
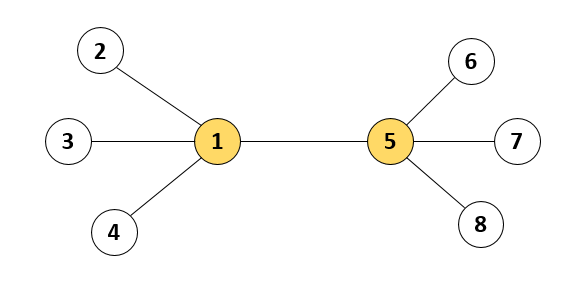
등대의 개수 n과 각 뱃길이 연결된 등대의 번호를 담은 이차원 배열 lighthouse가 매개변수로 주어집니다. 윤성이가 켜 두어야 하는 등대 개수의 최솟값을 return 하도록 solution 함수를 작성해주세요.
📝 풀이
#include <string>
#include <vector>
using namespace std;
vector<vector<int>> v;
bool light[100001] = {false, }; // 불이 켜진 등대인지 체크
int answer = 0;
// from: 어느 노드에서 왔는가?
// here: 현재 노드
void DFS(int from, int here)
{
// here(현재 위치)에서 갈 수 있는 모든 노드를 검사
for (int i = 0; i < v[here].size(); i++)
{
// 이전 노드(from)로 돌아가지 않아야 함
// DFS를 통해 무방향 탐색을 할경우 1 -> 2 -> 3 -> 2처럼 v[here][i] == from이 되는 경우가 있음
if (v[here][i] != from)
{
// 현재 위치에서 v[here][i]로 이동
DFS(here, v[here][i]);
// 만약 현재 위치와, 다음 위치 모두 불이 꺼져있는경우, 불을 켜면서, ++answer
if (!light[v[here][i]] && !light[here])
{
light[here] = true;
++answer;
}
}
}
}
int solution(int n, vector<vector<int>> lighthouse) {
v = vector<vector<int>>(n + 1, vector<int>());
// 무방향 그래프로 양쪽으로 이동할 수 있게 삽입
for(vector<int> path : lighthouse)
{
v[path[0]].push_back(path[1]);
v[path[1]].push_back(path[0]);
}
// 가상위치(0)에서 1번 노드로 이동하는것으로 탐색 시작
DFS(0, 1);
return answer;
}- DFS를 이용하여 문제를 해결하였습니다.
- 무방향 그래프로, 왕복할 수 있도록 v에 1 -> 2, 2 -> 1에 대하여 경로를 삽입해줘야합니다.
- 1번 노드부터 시작하여 DFS를 시작합니다.
- 현재 노드(here)에서부터 갈 수 있는 모든 노드를 검사합니다. 이때, here과 이전 노드(from)이 같다면, 말단 노드에 들렀다가 돌아온 경우로, 더 이상 진행하지 않습니다.
- 이 상태에서는 불에 대한 검사를 수행하지 않습니다. 말단 노드에서 불이 켜질 수 없습니다.
- 깊이 탐색 중 현재 노드와, 다음 노드가 둘 다 불이 꺼져있다면, 해당 위치에 불을 켜고, ++answer을 수행합니다.
'algorithms (C++)' 카테고리의 다른 글
| [C++][프로그래머스] 2차원 동전 뒤집기 (1) | 2023.11.26 |
|---|---|
| [C++][프로그래머스] 부대복귀 (0) | 2023.11.26 |
| [C++][프로그래머스] 숫자 타자 대회 🔥 (1) | 2023.11.25 |
| [C++][프로그래머스] 단체사진 찍기 (1) | 2023.11.20 |
| [C++][프로그래머스] 게임 맵 최단거리 (1) | 2023.11.20 |
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
📄 문제
인천 앞바다에는 1부터 n까지 서로 다른 번호가 매겨진 등대 n개가 존재합니다. 등대와 등대 사이를 오가는 뱃길이 n-1개 존재하여, 어느 등대에서 출발해도 다른 모든 등대까지 이동할 수 있습니다. 등대 관리자 윤성이는 전력을 아끼기 위하여, 이 중 몇 개의 등대만 켜 두려고 합니다. 하지만 등대를 아무렇게나 꺼버리면, 뱃길을 오가는 배들이 위험할 수 있습니다. 한 뱃길의 양쪽 끝 등대 중 적어도 하나는 켜져 있도록 등대를 켜 두어야 합니다.
예를 들어, 아래 그림과 같이 등대 8개와 7개의 뱃길들이 있다고 합시다. 이 경우 1번 등대와 5번 등대 두 개만 켜 두어도 모든 뱃길은 양쪽 끝 등대 중 하나가 켜져 있으므로, 배들은 안전하게 운항할 수 있습니다.

등대의 개수 n과 각 뱃길이 연결된 등대의 번호를 담은 이차원 배열 lighthouse가 매개변수로 주어집니다. 윤성이가 켜 두어야 하는 등대 개수의 최솟값을 return 하도록 solution 함수를 작성해주세요.
📝 풀이
#include <string>
#include <vector>
using namespace std;
vector<vector<int>> v;
bool light[100001] = {false, }; // 불이 켜진 등대인지 체크
int answer = 0;
// from: 어느 노드에서 왔는가?
// here: 현재 노드
void DFS(int from, int here)
{
// here(현재 위치)에서 갈 수 있는 모든 노드를 검사
for (int i = 0; i < v[here].size(); i++)
{
// 이전 노드(from)로 돌아가지 않아야 함
// DFS를 통해 무방향 탐색을 할경우 1 -> 2 -> 3 -> 2처럼 v[here][i] == from이 되는 경우가 있음
if (v[here][i] != from)
{
// 현재 위치에서 v[here][i]로 이동
DFS(here, v[here][i]);
// 만약 현재 위치와, 다음 위치 모두 불이 꺼져있는경우, 불을 켜면서, ++answer
if (!light[v[here][i]] && !light[here])
{
light[here] = true;
++answer;
}
}
}
}
int solution(int n, vector<vector<int>> lighthouse) {
v = vector<vector<int>>(n + 1, vector<int>());
// 무방향 그래프로 양쪽으로 이동할 수 있게 삽입
for(vector<int> path : lighthouse)
{
v[path[0]].push_back(path[1]);
v[path[1]].push_back(path[0]);
}
// 가상위치(0)에서 1번 노드로 이동하는것으로 탐색 시작
DFS(0, 1);
return answer;
}- DFS를 이용하여 문제를 해결하였습니다.
- 무방향 그래프로, 왕복할 수 있도록 v에 1 -> 2, 2 -> 1에 대하여 경로를 삽입해줘야합니다.
- 1번 노드부터 시작하여 DFS를 시작합니다.
- 현재 노드(here)에서부터 갈 수 있는 모든 노드를 검사합니다. 이때, here과 이전 노드(from)이 같다면, 말단 노드에 들렀다가 돌아온 경우로, 더 이상 진행하지 않습니다.
- 이 상태에서는 불에 대한 검사를 수행하지 않습니다. 말단 노드에서 불이 켜질 수 없습니다.
- 깊이 탐색 중 현재 노드와, 다음 노드가 둘 다 불이 꺼져있다면, 해당 위치에 불을 켜고, ++answer을 수행합니다.
'algorithms (C++)' 카테고리의 다른 글
| [C++][프로그래머스] 2차원 동전 뒤집기 (1) | 2023.11.26 |
|---|---|
| [C++][프로그래머스] 부대복귀 (0) | 2023.11.26 |
| [C++][프로그래머스] 숫자 타자 대회 🔥 (1) | 2023.11.25 |
| [C++][프로그래머스] 단체사진 찍기 (1) | 2023.11.20 |
| [C++][프로그래머스] 게임 맵 최단거리 (1) | 2023.11.20 |
